Certifying large prime numbers : a purely functional library for

$ 7.99 · 4.9 (233) · In stock

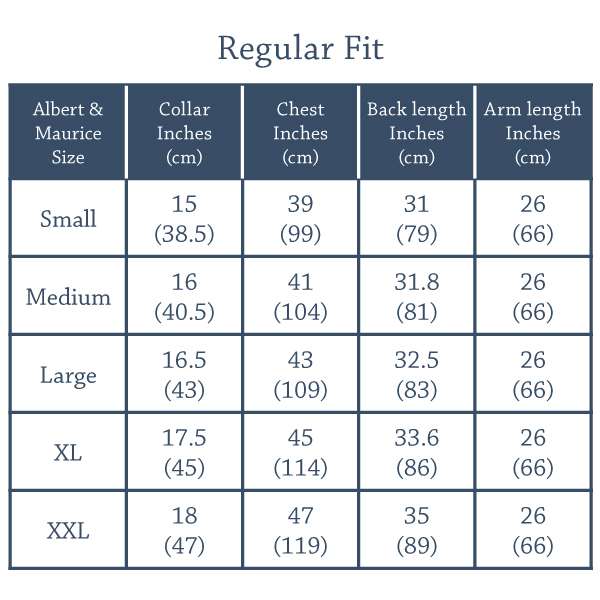
A library of modular arithmetic that has been developed within the Coq proof assistant and is purely functional but can be used on top of some native modular arithmetic, capable of certifying the primality of numbers with more than 44000 digits. Computing efficiently with numbers can be crucial for some theorem proving applications. In this paper, we present a library of modular arithmetic that has been developed within the Coq proof assistant. The library proposes the usual operations that have all been proved correct. The library is purely functional but can also be used on top of some native modular arithmetic. With this library, we have been capable of certifying the primality of numbers with more than 44000 digits. 1 Safe computation and prime numbers Recent formal developments such as [9, 17] have shown all the benefits one can get from having a formal system where both proving and computing are possible. In the Coq proof assistant [18], computation is provided by the logic. Coq is based on the Calculus of Inductive Construction, so the evaluation mechanism is given for free by the beta reduction rule. A direct application of the primitive status of computation is the so-called two-level approach [4]. To illustrate it, let us consider the problem of proving the primality of some natural numbers. Suppose that we have defined a predicate prime: a number is prime if it has exactly two divisors, one and itself. How do we now prove that 17 is prime? The standard approach is to directly build a proof object using tactics. Of course, this task can be automated writing an adhoc tactic. Still, behind the scene, the system will have to build a proof object and the larger the number to be proved prime is, the larger the proof term will be. The two-level approach proposes an alternative strategy in two steps. In the first step, one defines a function that expresses the problem in term of pure computation. It can be seen as a semi-decision procedure. In our case, it amounts in writing a function test from natural number to boolean such that the function returns true if the number is prime. For example, if the natural number is n, the function can check that there is no divisor between 2 and n− 1 by a simple iteration. In the second step, one proves that the function meets its specification ∀n, test n = true→ prime n So our semi-decision procedure is correct. Now to give a proof that 17 is prime, it is sufficient to prove that the function test applies to 17 returns true. As the function test directly evaluates inside Coq, this last proof is simply the reflexivity of equality. Using the two-level approach, we have just transfered the problem of building a large proof object into a conversion problem: showing that test 17 is convertible to true. The size of the proof object is then independent of the number to be proved prime. Recent progress in the evaluation mechanism [10] has also made this approach attractive from the point of view of efficiency. In [12] we have presented a more elaborated way of applying the two-level approach for proving primality. It is based on the notion of prime certificate and more precisely of Pocklington certificate. A prime certificate is an object that witnesses the primality of a number. The Pocklington certificates we have been using are justified by the following theorem given in [5]: Theorem 1. Given a number n, a witness a and some pairs (p1, α1), . . . , (pk, αk) where all the pi are prime numbers, let F1 = p1 1 . . . p αk k R1 = (n− 1)/F1 s = R1/(2F1) r = R1mod (2F1) it is sufficient for n to be prime that the following conditions hold: F1 is even, R1 is odd, and F1R1 = n− 1 (1) (F1 + 1)(2F 2 1 + (r − 1)F1 + 1) > n (2) an−1 = 1(mod n) (3) ∀i ∈ {1, . . . , k} gcd(a n−1 pi − 1, n) = 1 (4) r − 8s is not a square or s = 0 (5) For a prime number n, the list [a, p1, α1, p2, α2, . . . , pk, αk] represents its Pocklington certificate. Even if generating a certificate for a given n can be cpuintensive, verifying conditions 1-5 is an order of magnitude simpler. In fact, only the verification of conditions 1-5 is crucial for asserting the primality. It requires safe computation and is done inside Coq. The generation of the certificate is delegated to an external tool. This is a direct application of the skeptic approach described in [2, 13]. With respect to the standard approach for the same problem [7], the two-level approach gives a huge improvement in term of size of the proof object and in term of time. Figure 1 illustrates this on some small examples. Applying the twolevel approach to larger numbers (> 1000 digits) made us realize the algorithmic limitation of the arithmetic provided by Coq. This was particularly true when applying the Lucas-Lehmer test for proving the primality of Mersenne numbers, i.e. numbers that can be written as 2 − 1. Theorem 2. Let (Sn) be recursively defined by S0 = 4 and Sn+1 = S n − 2, for p > 2, 2 − 1 is prime if and only if (2 − 1)|Sp−2.